Vicente R. Rausell Lillo (Todos los derechos reservados)

¡ BIENVENIDOS !
A MI PÁGINA DE ASTRONOMÍA
EJE DE GRAVITACIÓN
EJE GRAVITACIONAL (EG)
" La distancia máxima que puede alcanzar el campo gravitatorio emitido por un foco energético activo, cómo ondas gravitacionales,. O, "La línea imaginaria gravitacional que puede expandir un cuerpo o masa gravitacional hasta el límite de su influencia ondulatoria o fuerza gravitatoria..
La longitud del EJE GRAVITACIONAL, en Kms, la podemos calcular por la teoría newtoniana,, bajo la fórmula :
EG (eje gravitacional) (kms) = 4,2E-19 (Km/kg) x M (kgs)
Siendo:
EG, la longitud del eje gravitacional en kms
4,2E-19 Km/Kg de distancia = (2Pí * valor numérico constante gravitación, 6,6738E-11 * 10E-9 kms), por kg, de masa gravitacional
M, = masa gravitacional, Kgs
Ahora bien: En todo sistema gravitacional ondulatorio, se deduce que:
"La longitud (kms), del eje gravitacional es proporcional a la longitud de órbita, igual a su longitud de onda, (Kms) o al período orbital (sgs) de todos y cada uno de los objetos o partículas contenidos en el mismo, (gravitación pasiva) de tal manera, que el cuadrado de la velocidad orbital media (Vo²) de cualquier punto u objeto de un sistema orbital, multiplicada por su longitud de órbita (Lo = 2Pí x semieje mayor) o, el cubo de su velocidad orbital (Vo (cubo)) multiplicada por su período ((t, en sgs)) , es igual a la longitud del eje gravitacional. del sistema" , es decir:
Vo² x Lo = EG (Eje gravitacional) ó, EG = Vo (cubo) x t (período en segundos)
Más allá de la longitud del eje de gravitación o campo gravitatorio, se forman los sistema múltiples.(binarios,etc)
La longitud del EJE GRAVITACIONAL, en Kms, la podemos calcular por la teoría newtoniana,, bajo la fórmula :
EG (eje gravitacional) (kms) = 4,2E-19 (Km/kg) x M (kgs)
Siendo:
EG, la longitud del eje gravitacional en kms
4,2E-19 Km/Kg de distancia = (2Pí * valor numérico constante gravitación, 6,6738E-11 * 10E-9 kms), por kg, de masa gravitacional
M, = masa gravitacional, Kgs
Ahora bien: En todo sistema gravitacional ondulatorio, se deduce que:
"La longitud (kms), del eje gravitacional es proporcional a la longitud de órbita, igual a su longitud de onda, (Kms) o al período orbital (sgs) de todos y cada uno de los objetos o partículas contenidos en el mismo, (gravitación pasiva) de tal manera, que el cuadrado de la velocidad orbital media (Vo²) de cualquier punto u objeto de un sistema orbital, multiplicada por su longitud de órbita (Lo = 2Pí x semieje mayor) o, el cubo de su velocidad orbital (Vo (cubo)) multiplicada por su período ((t, en sgs)) , es igual a la longitud del eje gravitacional. del sistema" , es decir:
Vo² x Lo = EG (Eje gravitacional) ó, EG = Vo (cubo) x t (período en segundos)
Más allá de la longitud del eje de gravitación o campo gravitatorio, se forman los sistema múltiples.(binarios,etc)
ÍNDICE
1.- FUNDAMENTOS; La Heliosfera
2.- LA ONDA DE CHOQUE NORMAL
3.- MOVIMIENTO LINEAL DE UN SISTEMA (VL)
3.1.- Velocidad, espacio y tiempo
3.2.- Relación de proporcionalidad
4.- LA CONSTANTE DE GRAVITACIÓN UNIVERSAL (G) Y EL EJE GRAVITACIONAL (EG) EN LA MECÁNICA NEWTONIANA.
5.- CÁLCULO DEL CONCEPTO TEÓRICO DE MASA
6.- LA VELOCIDAD TEÓRICA DE LA LUZ (c)
7.- MASA Y ENERGÍA
8..- EJE GRAVITACIONAL DE LA LUNA, TIERRA, SOL, VÍA LÁCTEA Y GALAXIA DE ANDRÓMEDA
2.- LA ONDA DE CHOQUE NORMAL
3.- MOVIMIENTO LINEAL DE UN SISTEMA (VL)
3.1.- Velocidad, espacio y tiempo
3.2.- Relación de proporcionalidad
4.- LA CONSTANTE DE GRAVITACIÓN UNIVERSAL (G) Y EL EJE GRAVITACIONAL (EG) EN LA MECÁNICA NEWTONIANA.
5.- CÁLCULO DEL CONCEPTO TEÓRICO DE MASA
6.- LA VELOCIDAD TEÓRICA DE LA LUZ (c)
7.- MASA Y ENERGÍA
8..- EJE GRAVITACIONAL DE LA LUNA, TIERRA, SOL, VÍA LÁCTEA Y GALAXIA DE ANDRÓMEDA
1.- FUNDAMENTOS
En mi libro, "Un juego llamado universo".(En web: ,"www.unjuegollamadouniverso" editado en octubre de 1998, desarrollo una teoría basada en la onda de choque normal, u ondas gravitacionales (igual a la que se forma en el agua cuando un barco navega, o arrojamos una piedra al agua) próxima a la formulada en 1910 por Emil Belot, en la que basaba su teoría nebular,--Teoría nebular iniciada por Descartes y más tarde por Laplace, en 1644,-- en las ondas formadas por el Sol hacia el ápex -- punto localizado en las inmediaciones de la constelación de Hércules y Lira-- hacia el que aparentemente se dirige el sistema solar.
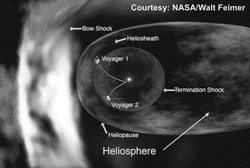
La Heliosfera
David McComas, del Southwest Research Institute en San Antonio, Texas, en un artículo publicado en la revista "Science". expone que:
"Si bien es cierto que hay arcos de choque por delante de muchas otras estrellas, estamos encontrando que la interacción de nuestro Sol no alcanza el umbral crítico para formar un shock, por lo que una onda de choque normal, es una representación más exacta de lo que está pasando por delante de nuestra heliosfera - exactamente igual que la onda formada por la proa de un barco que se desliza a través del agua "
http://www.swri.org/9what/releases/2012/bowshock.htm
David McComas, del Southwest Research Institute en San Antonio, Texas, en un artículo publicado en la revista "Science". expone que:
"Si bien es cierto que hay arcos de choque por delante de muchas otras estrellas, estamos encontrando que la interacción de nuestro Sol no alcanza el umbral crítico para formar un shock, por lo que una onda de choque normal, es una representación más exacta de lo que está pasando por delante de nuestra heliosfera - exactamente igual que la onda formada por la proa de un barco que se desliza a través del agua "
http://www.swri.org/9what/releases/2012/bowshock.htm
2.- LA ONDA DE CHOQUE NORMAL
Cuando sobre la superficie libre de un líquido, o un gas se propaga un movimiento ondulatorio sus partículas ejecutan movimientos periódicos de trayectoria circular . Esto es, sus vibraciones son a la vez longitudinales y transversales, formando un ángulo de 90 grados, perpendicular al eje horizontal, lo que es una onda de choque normal y son las que se forman cuando un barco navega, o cuando arrojamos una piedra al agua (a diferencia de las ondas de choque oblícuas, que describen un ángulo en la dirección del flujo, y el arco de choque, cuando supera una determinada velocidad superior al Mach, es decir, que alcance el umbral crítico del medio en que se mueve). Si la propagación de la perturbación no es superficial, las vibraciones de las partículas son cada vez más elípticas a profundidades crecientes con el eje mayor horizontal".
El principio ondulatorio de Huygens, también puede aplicarse cuando los centros de perturbación elementales no están en concordancia de fase, ya que por no pertenecer a una misma superficie de onda no han sido excitados simultáneamente.. De la más pequeña, a la más amplia, todas juntas forman un conjunto en forma de cono con vértice en el móvil, es la tangente o envolvente común (frente de ondas)
En este caso, es preciso trazar las ondas elementales correspondientes con radios diferentes con objeto de compensar las diferencias de fase de aquellos centros elementales.
Si el movimiento de un cuerpo tiene lugar con una velocidad, v, superior a la de la propagación de la perturbación mecánica en el medio u, entonces se dice que se mueve con velocidad supersónica respecto al medio de propagación, y si la velocidad relativa del movimiento del cuerpo con respecto al medio es inferior a aquella velocidad de las ondas, el movimiento recibe el nombre de subsónico. En ambos casos, todos los puntos intermedios han sido excitados sucesivamente, independientemente de las velocidades, pero en el primer caso, movimiento supersónico, la onda envolvente que se forma tendrá una estructura cónica, con vértice en la parte frontal del cuerpo, y cuya velocidad, u, es la velocidad de la onda de choque con radios desiguales, y en el segundo, movimiento subsónico, tendrá una estructura plana, es decir, unas ondas dentro de las otras. Si todos los puntos intermedios fueran excitados simultáneamente, obtendríamos una sucesión de ondas elementales de igual radio que tendría una envolvente común cilíndrica.
El principio ondulatorio de Huygens, también puede aplicarse cuando los centros de perturbación elementales no están en concordancia de fase, ya que por no pertenecer a una misma superficie de onda no han sido excitados simultáneamente.. De la más pequeña, a la más amplia, todas juntas forman un conjunto en forma de cono con vértice en el móvil, es la tangente o envolvente común (frente de ondas)
En este caso, es preciso trazar las ondas elementales correspondientes con radios diferentes con objeto de compensar las diferencias de fase de aquellos centros elementales.
Si el movimiento de un cuerpo tiene lugar con una velocidad, v, superior a la de la propagación de la perturbación mecánica en el medio u, entonces se dice que se mueve con velocidad supersónica respecto al medio de propagación, y si la velocidad relativa del movimiento del cuerpo con respecto al medio es inferior a aquella velocidad de las ondas, el movimiento recibe el nombre de subsónico. En ambos casos, todos los puntos intermedios han sido excitados sucesivamente, independientemente de las velocidades, pero en el primer caso, movimiento supersónico, la onda envolvente que se forma tendrá una estructura cónica, con vértice en la parte frontal del cuerpo, y cuya velocidad, u, es la velocidad de la onda de choque con radios desiguales, y en el segundo, movimiento subsónico, tendrá una estructura plana, es decir, unas ondas dentro de las otras. Si todos los puntos intermedios fueran excitados simultáneamente, obtendríamos una sucesión de ondas elementales de igual radio que tendría una envolvente común cilíndrica.
Para definir que onda de choque puede producir al avanzar un sistema en una nube local interestelar, veamos lo que sucede en una revolución.
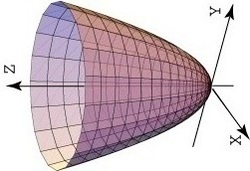
Calculamos primero la velocidad, u , de la onda, donde tenemos tres planos (tridimensional) X, Y, Z, (dibujo del cono)
Si, X = r. cos de alfa ; Y = r. sen de alfa, y
Z = C. r.
C es el número de revoluciones y r es el radio vector o la distancia al plano medio,. para calcular la proyección de la hélice sobre el plano YZ, tendremos,
para r = 1 ;
Z = TT´= 2Pi radianes.
tg de alfa = 2Pi / 1 ,
y la tg de delta (semiángulo) = 1 / 2Pi , por tanto,
alfa = arco tg (2 Pi ) / 1)
y delta = arco tg (1 / 2Pi ),
resolviendo alfa = 80,957 grados
y el semiángulo delta = 9,043 grados.
En radianes, alfa = 1,413 radianes y delta = 0,15783 radianes.
En la siguiente figura
Si, X = r. cos de alfa ; Y = r. sen de alfa, y
Z = C. r.
C es el número de revoluciones y r es el radio vector o la distancia al plano medio,. para calcular la proyección de la hélice sobre el plano YZ, tendremos,
para r = 1 ;
Z = TT´= 2Pi radianes.
tg de alfa = 2Pi / 1 ,
y la tg de delta (semiángulo) = 1 / 2Pi , por tanto,
alfa = arco tg (2 Pi ) / 1)
y delta = arco tg (1 / 2Pi ),
resolviendo alfa = 80,957 grados
y el semiángulo delta = 9,043 grados.
En radianes, alfa = 1,413 radianes y delta = 0,15783 radianes.
En la siguiente figura
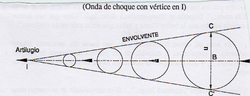
tg de alfa = BC (amplitud de la onda) /
IB (longitud), será igual a:
u (velocidad de la onda, km/sg) / Velocidad lineal o media, kms/sg;
Siendo delta = 9,043 grados, que es la anchura que el sistema forma en su conjunto
Luego tg 9,043 = BC / BI = u / VL kms/sg,
u = tg 9,043 . VL =, velocidad de la onda choque en kms/sg
Velocidad Inferior a su velocidad lineal (VL) lo que indica que su estructura es cónica, con un semiángulo de 9,043º sobre el plano de eclíptica y perpendicular al flujo, formando un ángulo de 90º, formando una envolvente común a todas ellas, (frente de ondas).
u (velocidad de la onda, km/sg) / Velocidad lineal o media, kms/sg;
Siendo delta = 9,043 grados, que es la anchura que el sistema forma en su conjunto
Luego tg 9,043 = BC / BI = u / VL kms/sg,
u = tg 9,043 . VL =, velocidad de la onda choque en kms/sg
Velocidad Inferior a su velocidad lineal (VL) lo que indica que su estructura es cónica, con un semiángulo de 9,043º sobre el plano de eclíptica y perpendicular al flujo, formando un ángulo de 90º, formando una envolvente común a todas ellas, (frente de ondas).
3.- MOVIMIENTO LINEAL DE UN SISTEMA (VL)
Es la velocidad lineal (VL) de un sistema en el espacio con respecto al sistema de reposo local (SRL)
3.1.- VELOCIDAD, LONGITUD Y TIEMPO
Para equilibrar los desfases de la onda de choque normal en una estructura cónica, la velocidad orbital media (Vo) de cada órbita debe ser mayor conforme se acerque al foco, y menor conforme se vayan alejando, con el fin de terminar sus ciclos respectivos todas al mismo tiempo. El centro del sistema no sufre alteración, el tiempo y la velocidad se equilibran, siendo el límite de separación entre ondas cortas y las largas , o sea, cuando obtengan una velocidad orbital media igual a su velocidad lineal (VL).
3.2.- RELACIÓN DE PROPORCIONALIDAD
Considerando en una órbita, el semieje mayor (r) ; el período de revolución (t) y la velocidad orbital media (Vo), que relaciona los dos conceptos anteriores, podemos decir que:
En relación a la velocidad lineal (VL) de un sistema, considerada como su velocidad orbital media, "El cuadrado de la velocidad orbital media (Vo), de cualquiera de sus elementos, es inversamente proporcional a su longitud de órbita (Lo) respectiva".
Sabiendo que la longitud de órbita (Lo) es igual a su semieje mayor (r) multiplicado por 2 Pí, (Lo = 2 Pí. r), y espacio es igual a velocidad por tiempo (Lo = Vot). Podemos formular, llamando al período de revolución de su velocidad lineal (velocidad orbital media del sistema) t (vl), que:
(Vo / VL)² = VL. t (vl) / Vo.t; resolviendo:
1) VL (al cubo) . t (vl) = Vo (al cubo). t.
El primer miembro de la igualdad, (VL (al cubo) . t (vl)), es la longitud del EJE GRAVITACIONAL (EG) en kilómetros, luego
1.1) EG = Vo (al cubo) . t (período de revolución en sgs)
Donde:
Primero.- La longitud en kilómetros cúbicos del eje gravitacional (EG) es igual al producto del cubo de la velocidad orbital media (Vo) de un punto cualquiera de un sistema, por el período de revolución en segundos (t), de dicho punto.
Y desglosando el segundo miembro de (1):
VL (al cubo) . t (vl) = Vo². (Vot)
2) VL (al cubo) . t (vl) = Vo² . Lo
2.1) EG = Vo². Lo
Segundo.- O, igual a la longitud calculada por el producto del cuadrado de la velocidad orbital media (Vo) de un punto cualquiera de un sistema, por la longitud de órbita (Lo) de dicho punto. También por su semieje mayor (r)
EG = 2П r vo²
Un punto cualquiera de un sistema es proporcional a su eje de gravitación.
En relación a la velocidad lineal (VL) de un sistema, considerada como su velocidad orbital media, "El cuadrado de la velocidad orbital media (Vo), de cualquiera de sus elementos, es inversamente proporcional a su longitud de órbita (Lo) respectiva".
Sabiendo que la longitud de órbita (Lo) es igual a su semieje mayor (r) multiplicado por 2 Pí, (Lo = 2 Pí. r), y espacio es igual a velocidad por tiempo (Lo = Vot). Podemos formular, llamando al período de revolución de su velocidad lineal (velocidad orbital media del sistema) t (vl), que:
(Vo / VL)² = VL. t (vl) / Vo.t; resolviendo:
1) VL (al cubo) . t (vl) = Vo (al cubo). t.
El primer miembro de la igualdad, (VL (al cubo) . t (vl)), es la longitud del EJE GRAVITACIONAL (EG) en kilómetros, luego
1.1) EG = Vo (al cubo) . t (período de revolución en sgs)
Donde:
Primero.- La longitud en kilómetros cúbicos del eje gravitacional (EG) es igual al producto del cubo de la velocidad orbital media (Vo) de un punto cualquiera de un sistema, por el período de revolución en segundos (t), de dicho punto.
Y desglosando el segundo miembro de (1):
VL (al cubo) . t (vl) = Vo². (Vot)
2) VL (al cubo) . t (vl) = Vo² . Lo
2.1) EG = Vo². Lo
Segundo.- O, igual a la longitud calculada por el producto del cuadrado de la velocidad orbital media (Vo) de un punto cualquiera de un sistema, por la longitud de órbita (Lo) de dicho punto. También por su semieje mayor (r)
EG = 2П r vo²
Un punto cualquiera de un sistema es proporcional a su eje de gravitación.
4.- LA CONSTANTE DE GRAVITACIÓN UNIVERSAL (G) Y EL EJE GRAVITACIONAL (EG) EN LA MECÁNICA NEWTONIANA
Por la fórmula
V² = G * M / r,
donde la constante G de la gravitación universal multiplicada por la masa (M) de un cuerpo y dividido por el radio orbital o distancia (r) , de otro cuerpo que orbite a su alrededor, obtenemos el cuadrado de su velocidad media orbital, podemos aplicar el valor numérico de dicha constante G (no su valor en-Newtons) en el cálculo del eje gravitacional (EG), en kilómetros, tomado como una medida de longitud, ya que se cumple que,
G (valor numérico) *10E-9) * M = EG / 2 Pí, y, por tanto
EG (kms) = 2 Pí * 6,6739E-20 (kms) * M, (kgs)
V² = G * M / r,
donde la constante G de la gravitación universal multiplicada por la masa (M) de un cuerpo y dividido por el radio orbital o distancia (r) , de otro cuerpo que orbite a su alrededor, obtenemos el cuadrado de su velocidad media orbital, podemos aplicar el valor numérico de dicha constante G (no su valor en-Newtons) en el cálculo del eje gravitacional (EG), en kilómetros, tomado como una medida de longitud, ya que se cumple que,
G (valor numérico) *10E-9) * M = EG / 2 Pí, y, por tanto
EG (kms) = 2 Pí * 6,6739E-20 (kms) * M, (kgs)
5.- CÁLCULO DEL CONCEPTO TEÓRICO DE MASA
Tomando como base la fórmula anterior (1) ,y tomando como constante el valor numérico del valor de G, el valor de la masa M, del foco o cuerpo central, sería, en Kgs
M (kgs) = EG / (2 Pí * 6,6739E-20) = EG / 4,2E-19
considerando, además, que por las fórmulas anteriores el eje gravitacional lo podemos calcular igualmente multiplicando el cuadrado de la velocidad orbital (V0) de cualquiera de sus elementos orbitales multiplicada por su longitud de órbita o, el cubo de la velocidad multiplicada por su período orbital, es decir:
M (kgs) = (Vo (cuadrado) * Lo) / 4,2E-19
Entonces, la masa (M) necesaria para obtener una unidad de eje, es la inversa de 4,19E-19,, o sea:
1 / 4,2E-19 = 2,38E+18 unidades de masa en kgs, de tal forma que una unidad:
1 = 4,2E-19 * 2,38E+18 Kgs
es decir, 2,38.10E9 unidades de masa por unidad de EG, se cumple que la masa (M) es igual a la masa inicial (MI) o unidad de masa en kgs, multiplicada por el eje gravitacional (EG), en kms
M (kgs) = 2,38.10E18 kgs * EG, de donde
EG (kms) = M / 2,38.10E18 kgs , y, por tanto
1 kg. de masa obtiene un campo gravitatorio de 4,2E-19 kms.de eje
M (kgs) = EG / (2 Pí * 6,6739E-20) = EG / 4,2E-19
considerando, además, que por las fórmulas anteriores el eje gravitacional lo podemos calcular igualmente multiplicando el cuadrado de la velocidad orbital (V0) de cualquiera de sus elementos orbitales multiplicada por su longitud de órbita o, el cubo de la velocidad multiplicada por su período orbital, es decir:
M (kgs) = (Vo (cuadrado) * Lo) / 4,2E-19
Entonces, la masa (M) necesaria para obtener una unidad de eje, es la inversa de 4,19E-19,, o sea:
1 / 4,2E-19 = 2,38E+18 unidades de masa en kgs, de tal forma que una unidad:
1 = 4,2E-19 * 2,38E+18 Kgs
es decir, 2,38.10E9 unidades de masa por unidad de EG, se cumple que la masa (M) es igual a la masa inicial (MI) o unidad de masa en kgs, multiplicada por el eje gravitacional (EG), en kms
M (kgs) = 2,38.10E18 kgs * EG, de donde
EG (kms) = M / 2,38.10E18 kgs , y, por tanto
1 kg. de masa obtiene un campo gravitatorio de 4,2E-19 kms.de eje
6.- LA VELOCIDAD TEÓRICA DE LA LUZ (C)
La velocidad teórica de la luz o velocidad del fotón, vendrá determinado en cada sistema por el punto de inflexión o longitud de órbita (Lo), que la velocidad orbital media (Vo) iguala a la velocidad (u) de la onda de choque, Así, despejando, Lo, de la fórmula general del Eje de gravitación.
Lo = EG / u (cuadrado) = c²
De igual manera, en el otro extremo, podemos calcular la velocidad media, Vo, que obtiene una longitud de órbita, (Lo) de u², de distancia del foco, es decir, de u (cuadrado) kms, con su semieje en la fotosfera y emisión de fotones), así:
Vo= c = Raíz ( EG / u (cuadrado) ) = velocidad de la luz
Luego:
c². u² = EG,
y
c² = EG / u² , donde
c = Raíz ( EG / u² )
Como ejemplo, la velocidad de la luz teórica que podemos calcular de esta manera en el sistema planetario binario "UPSILÓN ANDROMEDAE", situado en la constelación de Andrómeda, a unos 43,9 años luz de distancia de la Tierra, con una masa de 2,52*10E30 Kgs, (1,28 soles), calculado un EG de 1,0993*10E12 kms, con una velocidad media lineal de 20,452 kms/sg, (velocidad radial -28,9 kms/sg,), con una velocidad u, de la onda de choque de 3, 228 kms/sg, es de 324.803,42 Kms/sg.
Otro ejemplo notable es la velocidad que así obtenemos en el sistema "OGLE-TR-113" en la constelación Carina a unos 1800 años luz de la Tierra, con una masa de 1,55 * 10E30,kgs (0,78 soles), con una longitud de EG, de 6,51*10E11 kms, con una VL de 17,94 kms/sg. y una velocidad, u, de 2,831 kms/sg, se obtiene una velocidad luz de 284.945,29 Kms/sg
El cálculo de la velocidad de la luz (c), en nuestro sistema solar, de 299. 792,5, Kms/sg, se puede ver en la pestaña de esta página "EJE GRAVITACIONAL EN EL SISTEMA SOLAR".
Lo = EG / u (cuadrado) = c²
De igual manera, en el otro extremo, podemos calcular la velocidad media, Vo, que obtiene una longitud de órbita, (Lo) de u², de distancia del foco, es decir, de u (cuadrado) kms, con su semieje en la fotosfera y emisión de fotones), así:
Vo= c = Raíz ( EG / u (cuadrado) ) = velocidad de la luz
Luego:
c². u² = EG,
y
c² = EG / u² , donde
c = Raíz ( EG / u² )
Como ejemplo, la velocidad de la luz teórica que podemos calcular de esta manera en el sistema planetario binario "UPSILÓN ANDROMEDAE", situado en la constelación de Andrómeda, a unos 43,9 años luz de distancia de la Tierra, con una masa de 2,52*10E30 Kgs, (1,28 soles), calculado un EG de 1,0993*10E12 kms, con una velocidad media lineal de 20,452 kms/sg, (velocidad radial -28,9 kms/sg,), con una velocidad u, de la onda de choque de 3, 228 kms/sg, es de 324.803,42 Kms/sg.
Otro ejemplo notable es la velocidad que así obtenemos en el sistema "OGLE-TR-113" en la constelación Carina a unos 1800 años luz de la Tierra, con una masa de 1,55 * 10E30,kgs (0,78 soles), con una longitud de EG, de 6,51*10E11 kms, con una VL de 17,94 kms/sg. y una velocidad, u, de 2,831 kms/sg, se obtiene una velocidad luz de 284.945,29 Kms/sg
El cálculo de la velocidad de la luz (c), en nuestro sistema solar, de 299. 792,5, Kms/sg, se puede ver en la pestaña de esta página "EJE GRAVITACIONAL EN EL SISTEMA SOLAR".
7.- MASA Y ENERGÍA
De las fórmulas:
EG (eje gravitacional)
1) EG = Velocidad orbital media (Vo) ² * Lo (longitud de órbita)
En la masa M (kgs)
2) M (Kgs) = 2,38.10E18 * EG, sustituyendo EG
M= 2,38.10E18 * (Vo) ² * Lo
y en c (velocidad de la luz)
3) c² = EG / u², sustituyendo EG de 1)
c² = (Vo² * Lo) / u²
.Tenemos, que de la fórmula de Energía
E = m * c²
(1) E = m * EG / u (cuadrado)
y sustituyendo de 2) y de 3) queda
(2) E = 2,38*10E+18 * (Vo² * Lo)² / u², simplificando
E = (2,38.10E+18 * EG²) / u²
EG (eje gravitacional)
1) EG = Velocidad orbital media (Vo) ² * Lo (longitud de órbita)
En la masa M (kgs)
2) M (Kgs) = 2,38.10E18 * EG, sustituyendo EG
M= 2,38.10E18 * (Vo) ² * Lo
y en c (velocidad de la luz)
3) c² = EG / u², sustituyendo EG de 1)
c² = (Vo² * Lo) / u²
.Tenemos, que de la fórmula de Energía
E = m * c²
(1) E = m * EG / u (cuadrado)
y sustituyendo de 2) y de 3) queda
(2) E = 2,38*10E+18 * (Vo² * Lo)² / u², simplificando
E = (2,38.10E+18 * EG²) / u²
8.- EJE GRAVITACIONAL DE LA LUNA, TIERRA, SOL, VÍA LÁCTEA Y GALAXIA DE ANDRÓMEDA
MASA (kgs)-- --EJE (CAMPO) GRAVITACIONAL (kms)
LUNA 7,3E22 30.607,97
TIERRA 5,977E24 2.511.679,56
SOL 1,99E30 8,35E11
VÍA LÁCTEA 1,86E41 7,77E22
ANDRÓMEDA 2,59E42 1,08E24
LUNA 7,3E22 30.607,97
TIERRA 5,977E24 2.511.679,56
SOL 1,99E30 8,35E11
VÍA LÁCTEA 1,86E41 7,77E22
ANDRÓMEDA 2,59E42 1,08E24