EL EJE GRAVITACIONAL EN EL SISTEMA SOLAR
.
DOCUMENTAL: LA ARMONÍA DE LAS ESFERAS.
VÍDEO: LA MÚSICA DE LOS PLANETAS EN EL SISTEMA SOLAR:
ÍNDICE:
VÍDEOS:
.- DOCUMENTAL: LA MÚSICA DE LAS ESFERAS
.- "LA MELODÍA DE LOS PLANETAS EN EL SISTEMA SOLAR
1- LA BURBUJA SOLAR
2.- MOVIMIENTO SOLAR
3.- ESTRUCTURA
4.- ÓRBITAS: Semieje mayor
4.1.- Velocidades orbitales medias
4.2.- Ley de cuadrados
5.- CALCULA TÚ MISMO LOS DATOS DEL SISTEMA SOLAR POR SU EJE GRAVITACIONAL:
A.- Velocidad a distancia de 2Pí
B.- Centro pulsante
C.- Cálculo de la velocidad de la luz (c)
6.- CÁLCULO DE LA MASA DEL SOL
7.- EJE GRAVITACIONAL DE LOS PLANETAS
7.1.- Velocidades orbitales de las lunas
7.2.- Otos datos
8.- LA SONDA ESPACIAL "VOYAGER 1," EL 12 DE SEPTIEMBRE DE 2013
9.- DISTANCIAS
10.- LÍMITE DEL SISTEMA https://computerhoy.com/noticias/life/planeta-9-sistema-solar-tiene-tam
11.- PRESENTACIÓN EN OPPEN
12- PLANETA X
13.- VERSIONES ANTERIORES:
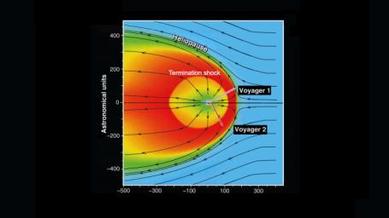
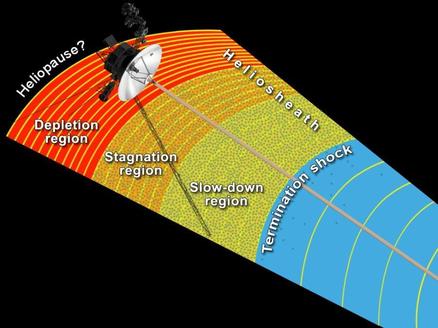
1.- LA BURBUJA SOLAR
.La imagen representa la burbuja solar, según los datos
enviados por las sondas espaciales Voyager 1 y Voyager 2, que se mueve a través
del espacio interestelar cercano o en el espacio entre las estrellas que
se muestra en azul, ya que se encuentra lleno de plasma o gas ionizado. El color
rojo indica temperaturas calientes superiores a 2 millones de grados. Las
líneas negras indican el flujo del viento solar dentro de la burbuja solar y el
flujo del viento interestelar en el espacio interestelar.
2.- MOVIMIENTO SOLAR
El movimiento solar es considerado como la velocidad lineal (VL) del sistema solar en el espacio y en dirección al ápex (punto de la esfera celeste) con respecto al sistema de reposo local (SRL). Se estima en una media de 19,1 km/sg, ó 42.726 kms/hora, (entre 16,5 y 23,2 kms/sg) la velocidad lineal del sistema solar, que aplico en el cálculo de su eje gravitacional (EG), y que confirma los datos del satélite científico IBEX (NASA Interstellar Boundary Explorer) el 10 de mayo de 2012, que demuestra que la heliosfera, o burbuja solar, al moverse a través de la nube interestelar local formando una onda de choque normal, actualmente, a una velocidad media de unas 52 mil millas por hora, es decir, 83.686 kms/hora, ó 23,2 kms/sg --- Esta velocidad es independiente de la velocidad orbital media del Sol alrededor de la galaxia de 217,39 kms/sg--
.
.
3.- ESTRUCTURA
¿Por qué es una onda de choque normal?.
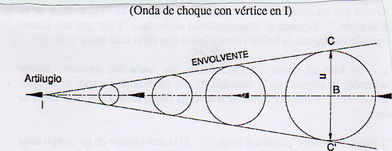
Siguiendo el cálculo anterior en la figura, tenemos que en nuestro sistema solar, considerando como velocidad media o velocidad lineal (VL) a 19,1 kms/sg, que
u = tg 9,043 . 19,1 = 3,04 kms/sg, como la velocidad de la onda choque
Velocidad Inferior a su velocidad lineal de 19,1 kms/sg. lo que indica que su estructura es cónica, con un semiángulo de 9,043º sobre el plano de eclíptica y perpendicular al flujo, formando un ángulo de 90º, como una onda de choque normal, ya que
2Pi . u = VL; y 2Pi. 3,04 kms/s = 19,1 kms/s
Esto se confirma, si multiplicamos los segundos que tardaría el Sol en recorrer la longitud de órbita de cualquier planeta a 19,1 kms/sg. por la velocidad de la onda de choque "u" de 3,04 kms/sg., donde su resultado será igual a la longitud de su semieje mayor. Por ejemplo: en el caso de la Tierra la longitud de órbita es de 939.966.720 kms. El Sol tardaría en recorrerlo
49.212.917,3 segundos, multiplicado. por 3,04 kms/sg. de velocidad, el espacio recorrido por la onda de choque al frente de ondas es de 149..607-269 kms. IGUAL A 1 UA., es decir igual a su semieje mayor. Igual sucede cn cualquier planeta u objeto de nuestro sistema solar.
El satélite científico IBEX que estudia la interacción
de nuestro Sistema Solar con el espacio exterior, reveló una nueva y sorprendente estructura en nuestro sistema planetario. Según publica en The Astrophisycal Journal.
Hasta ahora se trataba solo de una teoría. Las primeras imágenes del IBEX, en 2009, ya mostraban una especie de“cinta” hecha de átomos muy energéticos que rodeaba, por la parte exterior, todo nuestro sistema planetario. Fueron necesarios largos años de investigación para que la estructura a la que pertenecía esa “cinta” energética con un brillo cuatro veces más intenso que cualquier objeto celeste
| EN OPPEN,:UNA TEORÍA IMAGINARIA SOBRE SU FORMACIÓN . SU ESTRUCTURA. Y LÍMITES ppt | |
| File Size: | 2265 kb |
| File Type: | ppt |
VÍDEO PRINCIPIO Y FINAL DEL SISTEMA SOLAR.
4.- ÓRBITAS: Semieje mayor
Es evidente, que podemos calcular de esta manera los semiejes mayores de las órbitas por la velocidad lineal, VL, y la de ”u”, de la onda, al formar entre ellos un ángulo de 90º, calculando el tiempo (T), en segundos, que tardaría el Sol en recorrer cada longitud de órbita, formando el semieje mayor (r) (o amplitud de onda) de cada uno de los puntos del sistema, trazando así la envolvente común.
T = Lo (Longitud de órbita) / 19,1 Kms/sg
r (semieje mayor o amplitud de onda) = T . 3,04 Kms/sg (u)
El tiempo T, que tardaría el Sol en recorrer cada una de las longitud de órbita planetaria (semieje mayor por 2П) de nuestro sistema, es:
Mercurio: 19.083.769,6 sgs; Venus: 35.602.094,2 sgs; Tierra: 49.214.659,7 sgs; Marte: 75.026.178 sgs; Cinturón de asteroides: 119.973.682 sgs; Júpiter: 256.020.942 sgs; Saturno: 469.528.796 sgs; Urano: 944.502.618 sgs; Neptuno: 1.479.581.152 sgs; Plutón: 1.957.591.623 sgs; Sedna 24.736.520.667 sgs;
Tiempo, que multiplicado por la velocidad de la onda de choque, u , de 3,04 kms/sg, se obtiene los semiejes mayores o amplitud de onda, que en Unidades Astronómicas, son
Mercurio 0,387 UA; Venus 0,723 UA; Tierra 0,999 UA; Marte 1,523 UA; Cinturón de asteroides: 2,43 UA; Júpiter 5,2 UA; Saturno 9,53 UA; Urano 19,19 UA; Neptuno 30 UA; En el cinturón de Kuiper: Plutón 39,53 UA; Sedna 502,6 UA.
T = Lo (Longitud de órbita) / 19,1 Kms/sg
r (semieje mayor o amplitud de onda) = T . 3,04 Kms/sg (u)
El tiempo T, que tardaría el Sol en recorrer cada una de las longitud de órbita planetaria (semieje mayor por 2П) de nuestro sistema, es:
Mercurio: 19.083.769,6 sgs; Venus: 35.602.094,2 sgs; Tierra: 49.214.659,7 sgs; Marte: 75.026.178 sgs; Cinturón de asteroides: 119.973.682 sgs; Júpiter: 256.020.942 sgs; Saturno: 469.528.796 sgs; Urano: 944.502.618 sgs; Neptuno: 1.479.581.152 sgs; Plutón: 1.957.591.623 sgs; Sedna 24.736.520.667 sgs;
Tiempo, que multiplicado por la velocidad de la onda de choque, u , de 3,04 kms/sg, se obtiene los semiejes mayores o amplitud de onda, que en Unidades Astronómicas, son
Mercurio 0,387 UA; Venus 0,723 UA; Tierra 0,999 UA; Marte 1,523 UA; Cinturón de asteroides: 2,43 UA; Júpiter 5,2 UA; Saturno 9,53 UA; Urano 19,19 UA; Neptuno 30 UA; En el cinturón de Kuiper: Plutón 39,53 UA; Sedna 502,6 UA.
4.1.- VELOCIDADES ORBITALES MEDIAS
,
El eje gravitacional de nuestro sistema solar, o, la distancia máxima de la influencia gravitacional de nuestro Sol, dando valor numérico a la fórmula EG = (2Pí (valor numérico de G * 10E-9 * M = 4,2E-19 (kms) * M , siendo M, la masa del Sol,
EG = 4,2E-19 (kms)*1,989E+30 (kgs) = 8,35*10E11 kms
Y con la fórmula de proporcionalidad
VL(cubo) . t (vl) = Vo.
Como su VL de 19,1 kms/sg o velocidad media del sistema, y que el tiempo (t), o período es de 119.992.907,5 segundos, en ese punto situado en las proximidades de Vesta (Cinturón de asteroides), será, si 19,1 (al cubo) = 6967,8
(6967,8 . 119.992.905,5 sgs = 8,357.10E11 Kms = EG, que es la longitud del EJE GRAVITACIONAL (EG) de nuestro sistema solar
Las velocidades orbitales medias en cualquier punto de nuestro sistema, será:
1) Vo (kms/sg) = Raíz (8,35.10E11 / Lo (long. órbita) .
La misma proporción obtendremos, si operamos con los semiejes mayores de las órbitas de los planetas, al dividir dividendo y divisor por 2 П :
1.2) Vo (kms/sg) = Raíz ( 1,329.10E11 / Semieje mayor
También:
2) EG (Kms) = Período de revolución (sgs) . Vo (al cubo)
2.1) Vo (kms/sg) = Raíz cúbica (8,35.10E11 / Período (sgs))
Con estas fórmulas, comprobamos las velocidades orbitales medias de los planetas:
Mercurio: 47,9 kms/sg ; Venus 35,06 kms/sg; Tierra 29,8 kms/sg; Marte 24,15 kms/sg; En el cinturón de asteroides 19,1 kms/sg = MP; Júpiter 13,07 kms/sg; Saturno 9,65 kms/sg; Urano 6,8 kms/sg; Neptuno 5,43 kms/sg;
En el cinturón de Kuiper: Plutón 4,74 kms/sg; Eris 3,47 kms/sg y Sedna 1,33 kms/sg
EN LA HOJA DE CÁLCULO QUE SE ADJUNTA PUEDE CALCULAR LOS DATOS DE NUESTRO SISTEMA SOLAR POR EL EJE GRAVITACIONAL (EG)
4.2.- Ley de cuadrados
Todos los planetas, absolutamente todos los planetas tienen una forma redonda, o más precisamente hablando, esférica. Los planetas, las estrellas y los cometas no son ni cuadrados, ni rectangulares ni de ninguna otra forma, son esféricos. Pero ¿por qué los planetas son esféricos?
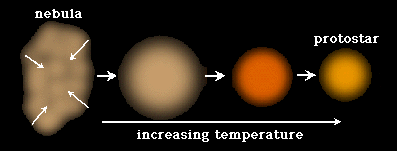
Los planetas tienen esta forma gracias a la fuerza de gravedad. La manera más sencilla de entender por qué ocurre esto es verlo desde la formación de un planeta.
La gravedad atrae de una u otra manera la materia en forma de polvo y gas, la cual se encuentra esparcida por el universo. Todo este polvo y gas forma una masa. Esta comienza a juntarse en torno al centro de gravedad , o centro de masa (cm), que ella misma forma.
Este centro gravitatorio hace que toda la masa se concentre hacia ella, y la única manera de que toda la materia esté lo más cerca posible de este centro gravitatorio es en forma esférica
Pero, ¿Por qué se ubican en unos lugares determinados del sistema gravitatorio..? ¿Es de una forma arbitraría, o de forma estrictamente matemática..?.
J.D.Titius y J.E. Bode, resumieron a finales del siglo XVIII, en una fórmula matemática la ley que lleva sus nombres La ley de Titius-Bode dice: “La distancia media, r, de un planeta al Sol, expresada en U.A. (Unidades Astronómicas. Una U.A.= 149,6 millones de Kms), es: r = 0,4 + 0,3 * 2n , siendo n, igual a (∞) en Mercurio, n = 0, en Venus; n = 1 para la Tierra; n = 2 para Marte; n = 3 para el valor medio de los Asteroides; n = 4 para Júpiter, etc. En el caso de Neptuno y Plutón aparece mayor discrepancia, al predecir, según la fórmula, 38,8 U.A. para Neptuno, cuando en realidad es de 30,5 U.A. y de 77,2 U.A. para Plutón, según la fórmula, cuando en realidad es de 39,7 U.A.
En realidad, el intervalo de los planetas se rigen por una ley matemática: La Ley de cuadrados; es decir: sus respectivos cuadrados, según sus intervalos de distancia entre ellos, considerando el tiempo transcurrido entre ellos (de uno al otro contiguo a la velocidad media del sistema de 19,1 kms(sg, desde Mercurio a Plutón ( Cinturón de Kuiper). Asi:
..- Intervalos de distancia
Calculando los Intervalos de distancia entre ellos sería (de mayor a menor distancia al Sol)
Intervalos de distancia a Plutón: a Neptuno (Idpn): 9,13155.109 Kms; Urano (Idpu): 1,93642.1010 Kms; a Saturno (Idps): 2,84244.1010 Kms; a Júpiter (Idpj):3,25024.1010 Kms; Centro pulsante (CP) (Idpcp): 3,510.1010 Kms; a Marte(Idpm): 3,596.1010 Kms; a Tierra (Idpt): 3,64522.1010 Kms; a Venus (Idpv): 3,6712.1010 Kms; a Mercurio (Idpme): 3,7.1010 Kms; y a I (idp), su longitud de órbita que hemos calculado de 3,739267.1010 Kms.
I
.- Intervalos de tiempo , .
Lo que tardaría el Sol a una velocidad media de 19,1 k,s/sg., en recorrer los intervalos de distancia entre cada planeta hasta el vértice del sistema
Bajo la fórmula:
Intervalo de tiempo (n) = Intervalos de distancia (n) /19,1 kms/sg
sería:
A Neptuno (Itpn): 4,781,108 segundos; a Urano (Itpu): 1,0138.109 sgs; a Saturno (Itps): 1,488.109 sgs; a Júpiter (Itpj): 1,7.109 sgs; a Centro Pulsante (CP (Itpcp)): 1,837.109 sgs; a Marte Itpm): 1,882.109 sgs; a Tierra (Itpt): 1,908.109 sgs; a Venus (Itpv): 1,922.109 sgs; a Mercurio (Itpme): 1,938.109 sgs; y al punto I Tiempo total invertido hasta Plutón (Itp) : 1,9577316.109 sgs.
.- Relación de intervalos (distancia y tiempo)
Con estos datos, la fórmula final de dicha relación (distancia y tiempo), sería:
Llamando R a dicha relación:
Dividir cada período,( Itpn, entre Itp), todo el tiempo que tarda en llegar el Sol al vértice del cono del sistema. Es decir: la proporción de distancia recorrida y tiempo transcurrido en cada intervalo desde Plutón (mayor distancia) hasta llegar a su vértice (Sol); es decir:
.
R = (Intervalo de distancia recorrida) / Idp (distancia total),
ó
Rp(n) = Itp(n) (intervalo de tiempo invertido) / Itp (período de tiempo total.)
Dicha relación de distancias y tiempo, en nuestro sistema, sería:
Desde Neptuno (Rpn) = 0,24 ( 24 %); Con Urano (Rpu) = 0,51 ( 51 %); Con Saturno (Rps) = 0,76 ( 76%); Con Júpiter (Rpj) = 0,87 ( 87 %); Con el CP (Rpcp) = 0,93 (93 %); Con Marte (Rpm) = 0,96 ( 96 %); Con Tierra (Rpt) = 0,974 ( 97 %); Con Venus (Rpv) = 0,9818 ( 98%); Con Mercurio (Rpme) = 0,99 ( 99 %), y al punto I, (Rp) = 1 ( 100 %)
Cómo o estamos calculando de mayor a menor distancia; es decir: desde el Cinturón de Kuiper (Plutón) hasta el vértice del cono( Sol) o inicio. Se puede calcular claramente que son su raíz respectivas entre cada uno de ellos. Luego, desde Mercurio a Plutón serán sus cuadrados.
De esta forma es evidente qué:
Rpn (Neptuno) es 0,24, y su raíz será 0,494; Rpu (Urano) es 0,51 (desvío 0,02), y su raíz es 0,72; Rps (Saturno) es 0,76, (desvío 0,04), y su raíz es 0,87; Rpj (Júpiter) es 0,87, (desvío 0), y su raíz es 0,93; Rpcp (Centro pulsante) es 0,93, (desvío 0), y su raíz es 0,96; Rpm (Marte) es 0,96, (desvío 0), y su raíz es 0,980; Rpt (Tierra) es 0,974, (desvío 0,006), y su raíz es 0,987; Rpv (Venus) es 0,9818, (desvío 0,006), y su raíz es 0,99; Rpme (Mercurio) es 0,99, (desvío 0) y el punto I, (Sol) o vértice del sistema cónico, es 1.
Empezando desde Mercurio, efectivamente serían sus cuadrados.
(Considerando la longitud de órbita excéntrica de Plutón, con respecto a los demás)
.5.- CALCULAR LOS DATOS DEL SISTEMA SOLAR POR EL EJE GRAVITACIONAL .
El eje gravitacional de nuestro sistema solar, o, la distancia máxima de la influencia gravitacional de nuestro Sol, dando valor numérico a la fórmula EG = (2Pí (valor numérico de G * 10E-9 * M = 4,2E-19 (kms) * M , siendo M, la masa del Sol,
EG = 4,2E-19 (kms)*1,989E+30 (kgs) = 8,35*10E11 kms
Y con la fórmula de proporcionalidad
VL(cubo) . t (vl) = Vo.
Como su VL de 19,1 kms/sg o velocidad media del sistema, y que el tiempo (t), o período es de 119.992.907,5 segundos, en ese punto situado en las proximidades de Vesta (Cinturón de asteroides), será, si 19,1 (al cubo) = 6967,8
(6967,8 . 119.992.905,5 sgs = 8,357.10E11 Kms = EG, que es la longitud del EJE GRAVITACIONAL (EG) de nuestro sistema solar
Las velocidades orbitales medias en cualquier punto de nuestro sistema, será:
1) Vo (kms/sg) = Raíz (8,35.10E11 / Lo (long. órbita) .
La misma proporción obtendremos, si operamos con los semiejes mayores de las órbitas de los planetas, al dividir dividendo y divisor por 2 П :
1.2) Vo (kms/sg) = Raíz ( 1,329.10E11 / Semieje mayor
También:
2) EG (Kms) = Período de revolución (sgs) . Vo (al cubo)
2.1) Vo (kms/sg) = Raíz cúbica (8,35.10E11 / Período (sgs))
Con estas fórmulas, comprobamos las velocidades orbitales medias de los planetas:
Mercurio: 47,9 kms/sg ; Venus 35,06 kms/sg; Tierra 29,8 kms/sg; Marte 24,15 kms/sg; En el cinturón de asteroides 19,1 kms/sg = MP; Júpiter 13,07 kms/sg; Saturno 9,65 kms/sg; Urano 6,8 kms/sg; Neptuno 5,43 kms/sg;
En el cinturón de Kuiper: Plutón 4,74 kms/sg; Eris 3,47 kms/sg y Sedna 1,33 kms/sg
EN LA HOJA DE CÁLCULO QUE SE ADJUNTA PUEDE CALCULAR LOS DATOS DE NUESTRO SISTEMA SOLAR POR EL EJE GRAVITACIONAL (EG)
4.2.- Ley de cuadrados
Todos los planetas, absolutamente todos los planetas tienen una forma redonda, o más precisamente hablando, esférica. Los planetas, las estrellas y los cometas no son ni cuadrados, ni rectangulares ni de ninguna otra forma, son esféricos. Pero ¿por qué los planetas son esféricos?
Los planetas tienen esta forma gracias a la fuerza de gravedad. La manera más sencilla de entender por qué ocurre esto es verlo desde la formación de un planeta.
La gravedad atrae de una u otra manera la materia en forma de polvo y gas, la cual se encuentra esparcida por el universo. Todo este polvo y gas forma una masa. Esta comienza a juntarse en torno al centro de gravedad , o centro de masa (cm), que ella misma forma.
Este centro gravitatorio hace que toda la masa se concentre hacia ella, y la única manera de que toda la materia esté lo más cerca posible de este centro gravitatorio es en forma esférica
Pero, ¿Por qué se ubican en unos lugares determinados del sistema gravitatorio..? ¿Es de una forma arbitraría, o de forma estrictamente matemática..?.
J.D.Titius y J.E. Bode, resumieron a finales del siglo XVIII, en una fórmula matemática la ley que lleva sus nombres La ley de Titius-Bode dice: “La distancia media, r, de un planeta al Sol, expresada en U.A. (Unidades Astronómicas. Una U.A.= 149,6 millones de Kms), es: r = 0,4 + 0,3 * 2n , siendo n, igual a (∞) en Mercurio, n = 0, en Venus; n = 1 para la Tierra; n = 2 para Marte; n = 3 para el valor medio de los Asteroides; n = 4 para Júpiter, etc. En el caso de Neptuno y Plutón aparece mayor discrepancia, al predecir, según la fórmula, 38,8 U.A. para Neptuno, cuando en realidad es de 30,5 U.A. y de 77,2 U.A. para Plutón, según la fórmula, cuando en realidad es de 39,7 U.A.
En realidad, el intervalo de los planetas se rigen por una ley matemática: La Ley de cuadrados; es decir: sus respectivos cuadrados, según sus intervalos de distancia entre ellos, considerando el tiempo transcurrido entre ellos (de uno al otro contiguo a la velocidad media del sistema de 19,1 kms(sg, desde Mercurio a Plutón ( Cinturón de Kuiper). Asi:
..- Intervalos de distancia
Calculando los Intervalos de distancia entre ellos sería (de mayor a menor distancia al Sol)
Intervalos de distancia a Plutón: a Neptuno (Idpn): 9,13155.109 Kms; Urano (Idpu): 1,93642.1010 Kms; a Saturno (Idps): 2,84244.1010 Kms; a Júpiter (Idpj):3,25024.1010 Kms; Centro pulsante (CP) (Idpcp): 3,510.1010 Kms; a Marte(Idpm): 3,596.1010 Kms; a Tierra (Idpt): 3,64522.1010 Kms; a Venus (Idpv): 3,6712.1010 Kms; a Mercurio (Idpme): 3,7.1010 Kms; y a I (idp), su longitud de órbita que hemos calculado de 3,739267.1010 Kms.
I
.- Intervalos de tiempo , .
Lo que tardaría el Sol a una velocidad media de 19,1 k,s/sg., en recorrer los intervalos de distancia entre cada planeta hasta el vértice del sistema
Bajo la fórmula:
Intervalo de tiempo (n) = Intervalos de distancia (n) /19,1 kms/sg
sería:
A Neptuno (Itpn): 4,781,108 segundos; a Urano (Itpu): 1,0138.109 sgs; a Saturno (Itps): 1,488.109 sgs; a Júpiter (Itpj): 1,7.109 sgs; a Centro Pulsante (CP (Itpcp)): 1,837.109 sgs; a Marte Itpm): 1,882.109 sgs; a Tierra (Itpt): 1,908.109 sgs; a Venus (Itpv): 1,922.109 sgs; a Mercurio (Itpme): 1,938.109 sgs; y al punto I Tiempo total invertido hasta Plutón (Itp) : 1,9577316.109 sgs.
.- Relación de intervalos (distancia y tiempo)
Con estos datos, la fórmula final de dicha relación (distancia y tiempo), sería:
Llamando R a dicha relación:
Dividir cada período,( Itpn, entre Itp), todo el tiempo que tarda en llegar el Sol al vértice del cono del sistema. Es decir: la proporción de distancia recorrida y tiempo transcurrido en cada intervalo desde Plutón (mayor distancia) hasta llegar a su vértice (Sol); es decir:
.
R = (Intervalo de distancia recorrida) / Idp (distancia total),
ó
Rp(n) = Itp(n) (intervalo de tiempo invertido) / Itp (período de tiempo total.)
Dicha relación de distancias y tiempo, en nuestro sistema, sería:
Desde Neptuno (Rpn) = 0,24 ( 24 %); Con Urano (Rpu) = 0,51 ( 51 %); Con Saturno (Rps) = 0,76 ( 76%); Con Júpiter (Rpj) = 0,87 ( 87 %); Con el CP (Rpcp) = 0,93 (93 %); Con Marte (Rpm) = 0,96 ( 96 %); Con Tierra (Rpt) = 0,974 ( 97 %); Con Venus (Rpv) = 0,9818 ( 98%); Con Mercurio (Rpme) = 0,99 ( 99 %), y al punto I, (Rp) = 1 ( 100 %)
Cómo o estamos calculando de mayor a menor distancia; es decir: desde el Cinturón de Kuiper (Plutón) hasta el vértice del cono( Sol) o inicio. Se puede calcular claramente que son su raíz respectivas entre cada uno de ellos. Luego, desde Mercurio a Plutón serán sus cuadrados.
De esta forma es evidente qué:
Rpn (Neptuno) es 0,24, y su raíz será 0,494; Rpu (Urano) es 0,51 (desvío 0,02), y su raíz es 0,72; Rps (Saturno) es 0,76, (desvío 0,04), y su raíz es 0,87; Rpj (Júpiter) es 0,87, (desvío 0), y su raíz es 0,93; Rpcp (Centro pulsante) es 0,93, (desvío 0), y su raíz es 0,96; Rpm (Marte) es 0,96, (desvío 0), y su raíz es 0,980; Rpt (Tierra) es 0,974, (desvío 0,006), y su raíz es 0,987; Rpv (Venus) es 0,9818, (desvío 0,006), y su raíz es 0,99; Rpme (Mercurio) es 0,99, (desvío 0) y el punto I, (Sol) o vértice del sistema cónico, es 1.
Empezando desde Mercurio, efectivamente serían sus cuadrados.
(Considerando la longitud de órbita excéntrica de Plutón, con respecto a los demás)
.5.- CALCULAR LOS DATOS DEL SISTEMA SOLAR POR EL EJE GRAVITACIONAL .
.Con el EG , podemos localizar o "pasear" por cualquier punto del sistema, bien por su velocidad orbital media, bien, por su longitud de órbita, por su semieje mayor, o por su período orbital, simplemente, despejando en la fórmulas indicadas. Y PUEDES CALCULARLO TÚ MISMO EN LA HOJA DE CÁLCULO QUE SE INSERTA.. Así, por ejemplo:
.A) - La velocidad con longitud de órbita de 2Pi
La velocidad que se obtiene a 1 km de distancia del centro del Sol, (Vo (cm), aplicando la fórmula,
Vo(cm) = Raíz (8,35.10E11 / 2П) = 364.734 kms/sg
B) .- Localizar el centro pulsante (CP) .
Podremos también obtener el punto que obtiene una longitud de órbita igual a la velocidad lineal de 19,1 kms/sg, como centro pulsante del sistema, despejando Lo, en la fórmula, tenemos:
1) 19,1² kms/sg = 8,35.10E11 kms / Lo (Long. órbita)
2) Lo = 8,35.10R11 kms / 364,73 = 2,29.10E9 kms
Con un semieje mayor de 364.734.208 kms, ó, 2,4 UA, situado en el cinturón de asteroides, en la proximidad de Vesta,.
C.- Velocidad de la luz (c):
Localizar la velocidad orbital de inflexión con la velocidad de la onda de choque, igual a 3,04 kms/sg.
El punto o la longitud de órbita (Lo), en que la velocidad orbital media (Vo) iguala a la velocidad (u) de la onda de choque, de 3,04 kms/sg, despejando, Lo
Lo = EG / u²
Lo = 8,35.10E11 / 3,04² = 8,99.10E10 kms. = c²
En este punto, muy importante, el semieje obtendrá 1,4 .10E10 kms, (8,99.10E10 / 2 Pí), a una distancia del sol de 95,617 UA y la Velocidad orbital de 3,04 kms/sg., punto llamado "Choque de terminación" lo que se denomina "el cruce" del viento solar (que se expande de manera radial y que según la NASA (datos del vehículo Ulyses en 1994-95) a una velocidad media de, aproximadamente, 400 kms/s, como final de la heliosfera y comienzo de la "heliopausa", en el interior de la nube de Oort.
De igual manera, en el otro extremo, podemos calcular la velocidad media, Vo, que obtiene una longitud de órbita, (Lo de u², de distancia del Sol, es decir, de 9,29 kms, a 1*10(-7) UA, con un semieje de 1,4 kms en la superficie solar (en la fotosfera y emisión de fotones)
Vo= c = Raíz ( 8,35.10E11 / 9,29 ) = 299.792,5 kms/sg = c = velocidad de la luz en nuestro sistema
.A) - La velocidad con longitud de órbita de 2Pi
La velocidad que se obtiene a 1 km de distancia del centro del Sol, (Vo (cm), aplicando la fórmula,
Vo(cm) = Raíz (8,35.10E11 / 2П) = 364.734 kms/sg
B) .- Localizar el centro pulsante (CP) .
Podremos también obtener el punto que obtiene una longitud de órbita igual a la velocidad lineal de 19,1 kms/sg, como centro pulsante del sistema, despejando Lo, en la fórmula, tenemos:
1) 19,1² kms/sg = 8,35.10E11 kms / Lo (Long. órbita)
2) Lo = 8,35.10R11 kms / 364,73 = 2,29.10E9 kms
Con un semieje mayor de 364.734.208 kms, ó, 2,4 UA, situado en el cinturón de asteroides, en la proximidad de Vesta,.
C.- Velocidad de la luz (c):
Localizar la velocidad orbital de inflexión con la velocidad de la onda de choque, igual a 3,04 kms/sg.
El punto o la longitud de órbita (Lo), en que la velocidad orbital media (Vo) iguala a la velocidad (u) de la onda de choque, de 3,04 kms/sg, despejando, Lo
Lo = EG / u²
Lo = 8,35.10E11 / 3,04² = 8,99.10E10 kms. = c²
En este punto, muy importante, el semieje obtendrá 1,4 .10E10 kms, (8,99.10E10 / 2 Pí), a una distancia del sol de 95,617 UA y la Velocidad orbital de 3,04 kms/sg., punto llamado "Choque de terminación" lo que se denomina "el cruce" del viento solar (que se expande de manera radial y que según la NASA (datos del vehículo Ulyses en 1994-95) a una velocidad media de, aproximadamente, 400 kms/s, como final de la heliosfera y comienzo de la "heliopausa", en el interior de la nube de Oort.
De igual manera, en el otro extremo, podemos calcular la velocidad media, Vo, que obtiene una longitud de órbita, (Lo de u², de distancia del Sol, es decir, de 9,29 kms, a 1*10(-7) UA, con un semieje de 1,4 kms en la superficie solar (en la fotosfera y emisión de fotones)
Vo= c = Raíz ( 8,35.10E11 / 9,29 ) = 299.792,5 kms/sg = c = velocidad de la luz en nuestro sistema
HOJA DE CÁLCULO PARA CALCULAR LA DISTANCIA AL SOL, EN UA, DE CUALQUIER PUNTO DEL SISTEMA POR SU VELOCIDAD ORBITAL MEDIA O LA VELOCIDAD ORBITAL MEDIA POR SU DISTANCIA AL SOL, EN UA, O CUALQUIER DATO DE NUESTRO SISTEMA SOLAR
| CALCULAR DATOS DEL SISTEMA SOLAR | |
| File Size: | 24 kb |
| File Type: | ods |
6.- CÁLCULO DE LA MASA DEL SOL
.Masa del Sol = 2,38.10E18 kgs (Masa inicial) . 8,35.10E11
kms (Eje Gravitacional) = 1.989.10E30 Kgs
Esta igualdad supone que cada 2,38.10E18 kgs de masa de forma constante, extiende 1 km de eje gravitacional. Esta fórmula se cumple al calcular los ejes gravitacioales de los planetas y de las estrellas en que se aplique.
Masa = 2,38.10E18 . EG , y
EG = M / 2,38.10R18
Esta igualdad supone que cada 2,38.10E18 kgs de masa de forma constante, extiende 1 km de eje gravitacional. Esta fórmula se cumple al calcular los ejes gravitacioales de los planetas y de las estrellas en que se aplique.
Masa = 2,38.10E18 . EG , y
EG = M / 2,38.10R18
7.- EJE GRAVITACIONAL DE LOS PLANETAS
Por la fórmula anterior y conocida la masa (M) de un planeta, podremos calcular su eje gravitacional (EGp), por el cociente de dividir, la masa del planeta (M) por la masa inicial (Mi).
EGp = M / 2,38.10E18 (MI)
Con esta fórmula obtenemos los ejes de simetría (EGp) de los planetas de nuestro sistemas solar:
Mercurio: Masa, 3,3.10E23 kgs, EGm 138.789,5 kms
Venus, Masa 4,87.10E24 kgs, EGv 2.045.798,32 kms
Tierra, Masa 5,974.10E24 kgs, EGt 2.500.000 kms
Marte, Masa 6,42.10E23, EGmt 269.747,9 kms
Júpiter, Masa 1,899.10E27, EGj 797.899.160 kms
Saturno, Masa 5,688.10E26 kgs, EGs 238.991.597 kms
Urano, Masa 8,686.10E25 kgs , EGu 3.649.579,83 kms
Neptuno 1,024.10E26 kgs, EGn 43.025.210,1 kms
En el cinturón de Kuiper:
Plutón, Masa 1,296.10E22 kgs. EGpt 5420,168 kms
Eris Masa 1,67.10E22 EGe 7016,8
Sedna, Masa 8,35.10E20, EGsd 351,134 kms
Por la longitud de los ejes de simetría de los planetas calculados, se puede obtener los mismos datos que el sistema.
EGp = M / 2,38.10E18 (MI)
Con esta fórmula obtenemos los ejes de simetría (EGp) de los planetas de nuestro sistemas solar:
Mercurio: Masa, 3,3.10E23 kgs, EGm 138.789,5 kms
Venus, Masa 4,87.10E24 kgs, EGv 2.045.798,32 kms
Tierra, Masa 5,974.10E24 kgs, EGt 2.500.000 kms
Marte, Masa 6,42.10E23, EGmt 269.747,9 kms
Júpiter, Masa 1,899.10E27, EGj 797.899.160 kms
Saturno, Masa 5,688.10E26 kgs, EGs 238.991.597 kms
Urano, Masa 8,686.10E25 kgs , EGu 3.649.579,83 kms
Neptuno 1,024.10E26 kgs, EGn 43.025.210,1 kms
En el cinturón de Kuiper:
Plutón, Masa 1,296.10E22 kgs. EGpt 5420,168 kms
Eris Masa 1,67.10E22 EGe 7016,8
Sedna, Masa 8,35.10E20, EGsd 351,134 kms
Por la longitud de los ejes de simetría de los planetas calculados, se puede obtener los mismos datos que el sistema.
7.1.- Velocidades orbitales de las lunas
.Las velocidades orbitales medias
de sus lunas (Vo)(l) podemos calcularlas por la fórmula de proporcionalidad.
Vo(l) = Raíz (EGp / long.órbita satélite, o, también
Vo(l) = Raíz cúbica (EGp / período (sgs)
Vo(l) = Raíz (EGp / long.órbita satélite, o, también
Vo(l) = Raíz cúbica (EGp / período (sgs)
7.2.- Otros datos
..- Su velocidad lineal (VLp)
VLp= Raíz (Vo(cm) /100), sabiendo, Vo(cm) = Raíz (ESp / 2П)
.- Su velocidad de onda de choque (Up)
up = VLp / 2П
VLp= Raíz (Vo(cm) /100), sabiendo, Vo(cm) = Raíz (ESp / 2П)
.- Su velocidad de onda de choque (Up)
up = VLp / 2П
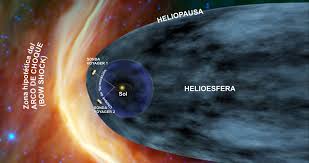
8- LA SONDA ESPACIAL, VOYAGER 1, EL 12 DE SEPTIEMBRE DE 2013
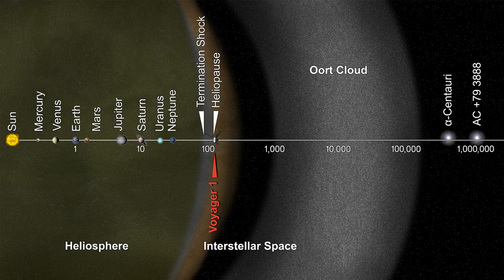
Es la nave espacial más distante de la humanidad, está alrededor de 125 UA. (el 12-09-2013) de la Tierra. Los científicos creen que entró en el espacio interestelar, o el espacio entre las estrellas, el 25 de agosto de 2012. Gran parte del espacio interestelar es en realidad dentro de nuestro sistema solar. Tomará cerca de 300 años para que la Voyager 1 pueda alcanzar el borde interior de la Nube de Oort y posiblemente unos 30.000 años para volar más allá de ella.
Alfa Centauri es actualmente la estrella más cercana a nuestro sistema solar. Sin embargo, en 40.000 años, Voyager 1 estará más cerca de la estrella AC +79 3888 que a nuestro propio sol. AC 79 3888 es en realidad viaja más rápido hacia la Voyager 1 de la nave espacial está viajando hacia allí.
Las naves espaciales Voyager 1 y 2, fueron construidas y continúan siendo operado por el Laboratorio de Propulsión a Chorro de la NASA, en Pasadena, California Caltech dirige el JPL para la NASA. Las misiones Voyager son una parte del sistema de Heliofísica de la NASA Observatorio, patrocinado por la División del Directorio de Misiones Científicas de la NASA en Washington Heliofísica.
Alfa Centauri es actualmente la estrella más cercana a nuestro sistema solar. Sin embargo, en 40.000 años, Voyager 1 estará más cerca de la estrella AC +79 3888 que a nuestro propio sol. AC 79 3888 es en realidad viaja más rápido hacia la Voyager 1 de la nave espacial está viajando hacia allí.
Las naves espaciales Voyager 1 y 2, fueron construidas y continúan siendo operado por el Laboratorio de Propulsión a Chorro de la NASA, en Pasadena, California Caltech dirige el JPL para la NASA. Las misiones Voyager son una parte del sistema de Heliofísica de la NASA Observatorio, patrocinado por la División del Directorio de Misiones Científicas de la NASA en Washington Heliofísica.
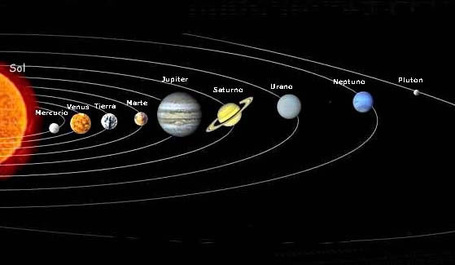
9- DISTANCIAS
..
La imagen pone distancias en el sistema
solar en perpectiva reducida reproducida por la NASA. La barra de escala es en
unidades astronómicas, con cada conjunto de distancia más allá de 1 UA
representa 10 veces la distancia anterior. Una UA es la distancia del Sol a la
Tierra, que es aproximadamente 150 millones de kilómetros (exactamente
149.597.870 kms). Neptuno, el planeta más distante del Sol, es de 30 UA. Más
allá de Neptuno, en el cinturón de Kuiper, tomando como referencia a Plutón (considerado como un planetoide) la
distancia es de 39,53 UA.
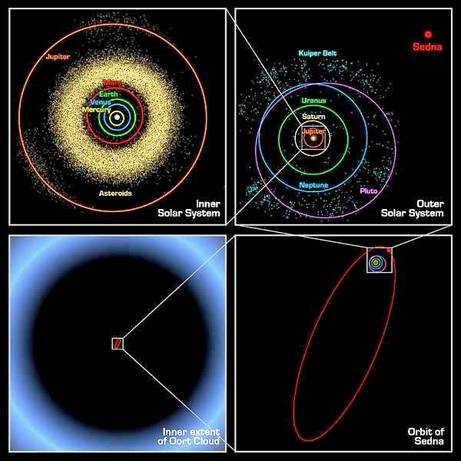
Informalmente, el término "sistema solar" se utiliza a menudo para significar el espacio hasta el último planeta. El consenso científico, sin embargo, dice que el sistema solar está con la nube de Oort, la fuente de los cometas que se mueven por nuestro sol en grandes escalas de tiempo. Más allá del borde exterior de la Nube de Oort, la gravedad de otras estrellas comienza a dominar a la del sol.
El borde interior de la parte principal de la Nube de Oort podría estar tan cerca como 1000 UA de nuestro sol. (Según el Eje gravitacional, la influencia de la atracción gravitacional del Sol es de 889,1 UAl y el borde exterior se estima en alrededor de 95,7 UA. (`punto de inflexión con la onda de choque)
http://www.nasa.gov/voyager y http://voyager.jpl.nasa.gov .
Considerando los cálculos obtenidos por el eje gravitacional estas distancias serían:
En la Heliosfera:
Del Sol a Mercurio: 0,387 UA;
De Mercurio al cinturón asteroides: 2 UA;
De los asteroides al cinturón de Kuiper: 37 UA
Total en la Heliosfera: 39,387 UA
Heliosfera al espacio interestelar de 39,387 UA a 95,617 UA = 56,23, UA
Espacio Interestelar al interior de la Nube de Oort: 793,48 UA
TOTAL 889,1 UA; que son 1329. 10E11 Kms.
Corresponde a la distancia media del Sol al límite de la influencia gravitacional del sistema (8,35.10E11 Kms / 2Pi).
Informalmente, el término "sistema solar" se utiliza a menudo para significar el espacio hasta el último planeta. El consenso científico, sin embargo, dice que el sistema solar está con la nube de Oort, la fuente de los cometas que se mueven por nuestro sol en grandes escalas de tiempo. Más allá del borde exterior de la Nube de Oort, la gravedad de otras estrellas comienza a dominar a la del sol.
El borde interior de la parte principal de la Nube de Oort podría estar tan cerca como 1000 UA de nuestro sol. (Según el Eje gravitacional, la influencia de la atracción gravitacional del Sol es de 889,1 UAl y el borde exterior se estima en alrededor de 95,7 UA. (`punto de inflexión con la onda de choque)
http://www.nasa.gov/voyager y http://voyager.jpl.nasa.gov .
Considerando los cálculos obtenidos por el eje gravitacional estas distancias serían:
En la Heliosfera:
Del Sol a Mercurio: 0,387 UA;
De Mercurio al cinturón asteroides: 2 UA;
De los asteroides al cinturón de Kuiper: 37 UA
Total en la Heliosfera: 39,387 UA
Heliosfera al espacio interestelar de 39,387 UA a 95,617 UA = 56,23, UA
Espacio Interestelar al interior de la Nube de Oort: 793,48 UA
TOTAL 889,1 UA; que son 1329. 10E11 Kms.
Corresponde a la distancia media del Sol al límite de la influencia gravitacional del sistema (8,35.10E11 Kms / 2Pi).
10.- LÍMITE DEL SISTEMA
.
t
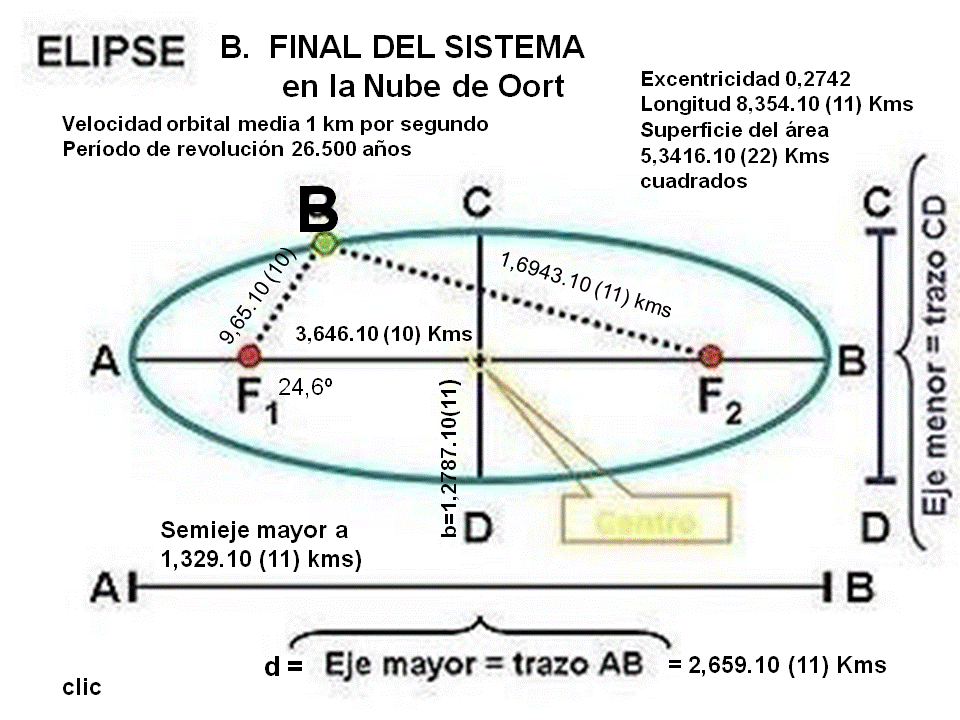
El final teórico de la influencia gravitacional de nuestro sistema solar, según el cálculo del eje gravitacional se encontraría a una distancia media de 132.900 millones de kms del Sol, a 889,1 UA, lo que un nuevo estudio demostraría la existencia de este nuevo y último planeta que en octubre de 2019, la NASA, lo definió como un agujero negro a una distancia del Sol, igual a la distancia del centro al foco F1 de la órbita B, de 250 veces una UA, lo que equivale a 3,65 por 10 (elevado a 10) La elipse B teórica de la figura, situaría la órbita de un supuesto planeta ahora definido como un agujero negro, con una velocidad orbital media teórica de 1 km/sg, con movimiento retrógrado.
Seguir el siguiente ENLACE DEL DESCUBRIMIENTO DE LA ÓRBITA b
https://computerhoy.com/noticias/life/planeta-9-sistema-solar-tiene-tam FOTO DEL PLANETA EN LA ÓRBITA B (AGUJERO NEGRO(
11.- PRESENTACIÓN EN OPPEN.
| UN PASEO POR EL SISTEMA SOLAR.ppt | |
| File Size: | 1295 kb |
| File Type: | ppt |
12.- PLANETA "X"
." El planeta X, demasiado lejano como para ser detectado por telescopios, delata su presencia al «alterar las órbitas de los objetos del cinturón de Kuiper», afirma Rodney Gomes, astrónomo del Observatorio Nacional de Brasil, en Río de Janeiro.
NOTA.- EN OCTUBRE DE 2019, SE CONFIRMA LA EXISTENCIA DEL PLANETA X,, EXACTAMENETE EN LA ÓRBITA B, DEL TAMAÑO DE UNA PELOTA DE TENIS Y SE DEFINE COMO UN AGUJERO NEGRO.
"Los cuerpos del cinturón de Kuiper son pequeños objetos helados, incluidos algunos planetas enanos, que se encuentran más allá de la órbita de Neptuno.
El planeta enano Plutón, por ejemplo, considerado una vez el noveno planeta de nuestro Sistema Solar, es uno de los cuerpos más grandes del cinturón de Kuiper, con 2.300 kilómetros de diámetro.
Hay otros cuerpos de cientos de kilómetros, y se descubren más cada año".
Según Gomes, lo curioso es que, basándose en sus nuevos cálculos, aproximadamente media docena de cuerpos del cinturón de Kuiper, incluido el lejano Sedna, se encuentra en órbitas extrañas, si lo comparamos con dónde deberían estar según los modelos existentes...."
«....La situación de sus órbitas tiene varias posibles explicaciones», señala Gomes, que presentó su descubrimiento el uno de octubre de 2013, en una reunión de la Sociedad Astronómica Americana en Oregón (Estados Unidos)...."
«....Pero creo que la más sencilla es la existencia de un planeta que orbita muy lejos del Sol pero que es suficientemente masivo como para provocar efectos gravitacionales en los cuerpos del cinturón de Kuiper».
Para su estudio, Gomes analizó las órbitas de 92 cuerpos del cinturón de Kuiper y comparó los resultados con simulaciones por ordenador de cómo debían estar distribuidos los objetos con y sin el nuevo planeta.
Sin él, la conclusión del científico fue que las simulaciones no producen las órbitas tan alargadas como las que vemos en seis de los cuerpos.
Lo que no está claro es cómo de grande sería exactamente el planeta, pero hay muchas posibilidades, según Gomes. Basándose en sus estimaciones, Gomes cree que encajaría la idea de un planeta del tamaño de Neptuno, de unas cuatro veces el tamaño de la Tierra, que orbitaría a 225 mil millones de kilómetros del Sol (aproximadamente 1.500 veces más lejos que la Tierra), según Gomes...."
***¡OJO!. ***
El eje de simetría lo sitúa a 132.900 millones de kilómetros del Sol. Si su órbita se encontrara a 225 mil millones de kilómetros del Sol, estaríamos en un SISTEMA BINARIO, como se ha calculado en otros sistemas planetarios (Ver en esta página la pestaña "Sistemas planetarios de 2,3,4 y 5 planetas", los sistemas binarios) .
Según este estudio, se trataría de un planeta muy apagado, y hay que tener en cuenta que las simulaciones llevadas a cabo por el equipo no proporciona ninguna pista para saber hacia donde dirigir los telescopios.. “Podría estar en cualquier sitio” afirma Gomes.
En cualquier caso, encontrarlo es todo un reto.
13..- VERSIÓN ANTERIOR COMPLETA PARA SU LECTURA (año 1998)
| AL LECTOR.pdf | |
| File Size: | 53 kb |
| File Type: | |
| 1.-INICIO. SU ESTRUCTURA POR EL MOVIMIENTO ONDULATORIOi..PDF | |
| File Size: | 2449 kb |
| File Type: | |
| 2.-SUCESIÓN PLANETARIA Y FASES.pdf | |
| File Size: | 1565 kb |
| File Type: | |
| 3_LÍMITES-FINAL Y SATÉLITES.pdf | |
| File Size: | 899 kb |
| File Type: | |
EXPRESA TU OPINIÓN
CONTACTA Y PARTICIPA
e-mail